امتدادات فيبوناتشي

تعلم الفوركس
يُعَد ليوناردو بيغوللو بيزانو، المعروف أيضًا بفيبوناتشي، واحد من أعظم علماء الرياضيات في أوروبا في العصور الوسطى (476 م - 1453 م). وقد كانت لرحلاته الكثيرة في طفولته في منطقة البحر المتوسط مع والده التاجر عظيم الأثر في تعريفه بالكثير من الوسائل المختلفة للرياضيات والمحاسبة. مع أنه أرسى دعائم الرياضة التجارية والرياضة المالية، لكنَّ أشهر ما يُعرف به اليوم هو أرقام ومتوالية فيبوناتشي.
وقد تطرق فيبوناتشي في كتابه "ليبر أباتشي" (ومعناه "كتاب الحساب") إلى مسألة عدد الأرانب التي يمكن إنتاجها في سنة واحدة إذا وُضِعَ زوج من الأرانب في قفصٍ، وولد كل زوج منها زوجًا جديدًا كل شهر (باستثناء ألا يلد كل زوج منها للمرة الأولى إلا بعد مرور شهرين)، وهو السؤال الذي جعله يتوصل إلى متوالية فيبوناتشي.
متوالية فيبوناتشي
تُشتق هذه المتوالية عن طريق جمع الرقمين السابقين على بعضهما للحصول على الرقم التالي لهما:

للحصول على رقم فيبوناتشي التالي في المتوالية، يُضاف 233 إلى 377 لنحصل على 610.
المهم بشأن هذا النمط هو أن نسبة أي رقم إلى الرقم السابق عليه مباشرة في المتوالية تميل لأن تكون 1.618، وهو الرقم الذي يشتهر بالنسبة الذهبية، ويُرمَز إليه بالحرف اللاتيني φ.
الهندسة
توجد في الهندسة نقطة على أي خط مستقيم، وهذه النقطة:
أ/ب = أ+ب/أ = φ = 1.618
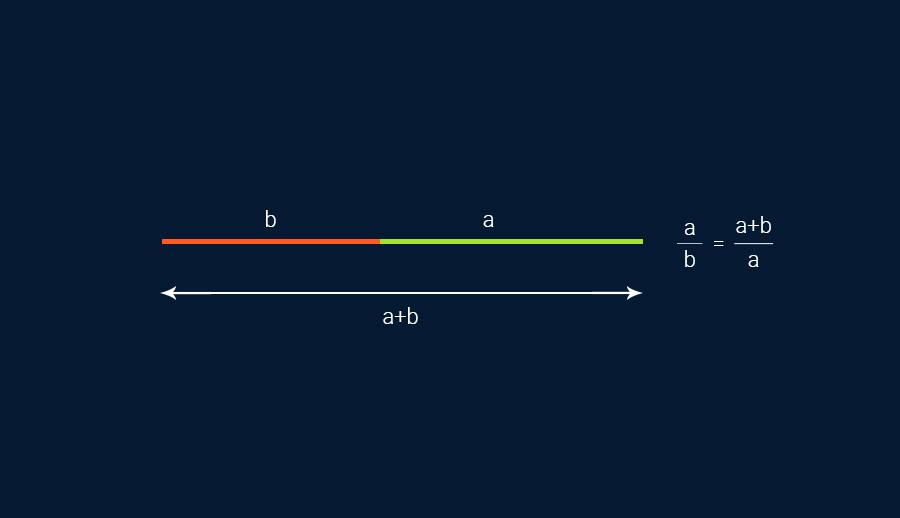
بالمثل، توجد هذه النسبة في مستطيلات ذهبية بضلع أ (الضلع الطويل) والضلع ب (الضلع القصير):

عندما توضع بجوار مربع طول أضلاعه أ، فإن نسبة الضلع الأطول (أ+ب) إلى الضلع الأقصر (ب) هي نفس نسبة الضلع ب في المستطيل الأطول إلى الضلع ب في المستطيل الأقصر، وهي تساوي المتوسط الذهبي (1.618).
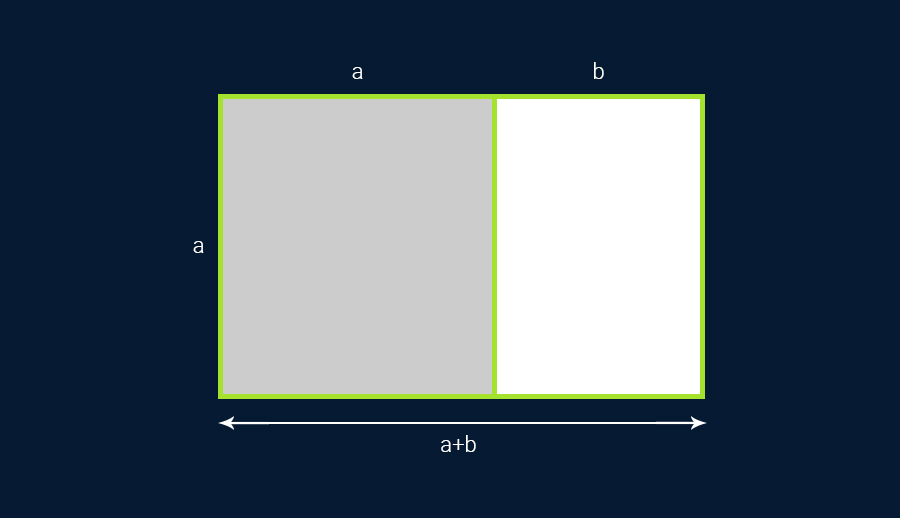
بالمثل، تتألف مستطيلات فيبوناتشي من مربعات تمثل أضلاعها أرقام فيبوناتشي.
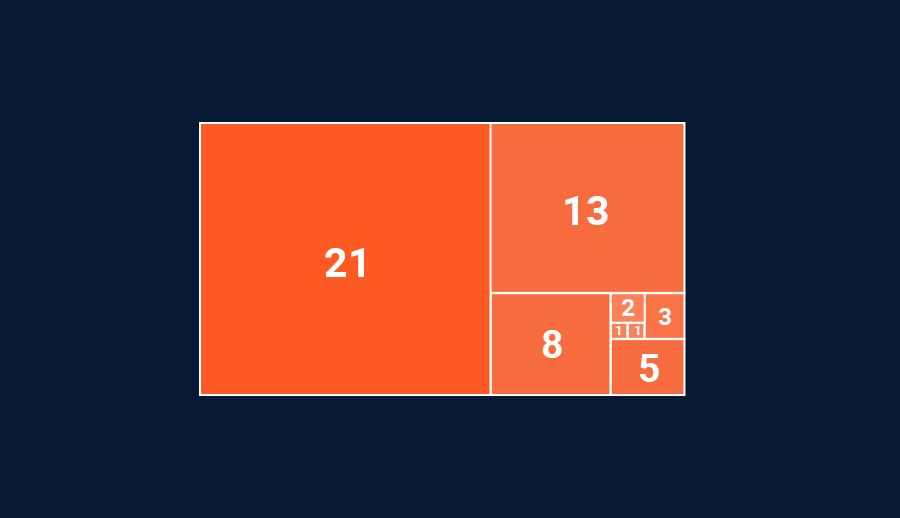
الهندسة المعمارية
النسبة الذهبية (التي تعرف أيضًا بالقسم الذهبي أو المتوسط الذهبي) لا يظهر في الهندسة فحسب، بل وفي المعمار أيضًا. كانت تُعَد نسبة الطول إلى العرض التي تساوي 1.618 بالتقريب الأكثر راحة للعينين عند الإغريق القدامى، بمن فيهم النحات الإغريقي فيدياس.

الرياضيات
في الرياضيات، تتسم النسبة الذهبية بالخصائص الفريدة الآتية:
1/Φ +1=Φ=1/(Φ+1)
Φ2 =Φ+1
Φ2 – Φ -1 =0 (حل المعادلة لإيجاد φ=1+sqrt(5) / 2)
الطبيعة
من المدهش بما يكفي أن الأزهار والنباتات أيضًا تتبع متوالية فيبوناتشي. على سبيل المثال، توجد في زهرة الماريبوسا ثلاث بتلات،

بينما توجد في زهرة الحوذان خمس بتلات صفراء لامعة.

تستمر هذه المتوالية بأمثلة من الأزهار تشمل 8 و13 و21 و34 بتلة وهكذا.
جسم الإنسان
كذلك توجد هذه النسبة في جسم الإنسان. على سبيل المثال، النسبة بين عرض القواطع الوسطية والقواطع الجانبية هي النسبة الذهبية.

امتدادات فيبوناتشي
كما رأينا، فإن ناتج قسمة أي رقم في المتوالية على الرقم السابق عليه هو 1.618. كذلك، فإن ناتج قسمة أي رقم في المتوالية على الرقم الأقل منه بمكانين هو 2.618. وأيضًا، فإن ناتج قسمة أي رقم في المتوالية على الرقم الأقل منه بثلاثة أماكن هو 4.236. تُسمى هذه النسب أيضًا امتدادات فيبوناتشي.
الأسواق المالية
ليست الأسواق المالية والتداول ببعيدين عن هذا الانتشار لنسب فيبوناتشي. يمكن أن تُستَخدَم نسب فيبوناتشي، أو امتدادات فيبوناتشي بأكثر تحديدًا، في المساعدة على تقدير المستهدفات السعرية المحتملة ومستويات جني الربح وإيقاف الخسارة.
على سبيل المثال، يمكن احتساب ثلاثة مستهدفات سعرية باستخدام أداة فيبوناتشي الموجودة أعلى الرسم وسحبها إلى الأسفل، وهذه المستهدفات هي: 1.618 و2.618 و4.236. هذه المستويات هي مستهدفات محتملة إلى الأعلى.
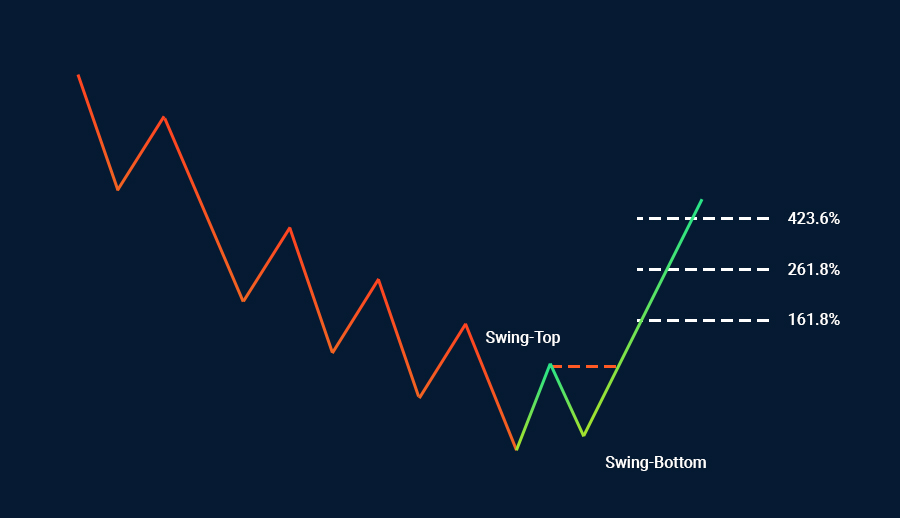
بالعكس، إذا استخدمنا أداة فيبوناتشي على التأرجح إلى الأسفل، نستطيع أيضًا احتساب ثلاثة مستهدفات محتملة للربح. يتم تثبيت أداة فيبوناتشي في أسفل التأرجح، ثم سحبها إلى أعلى التأرجح لاحتساب المستهدفات السعرية المقابلة: 1.618 و2.618 و4.236.
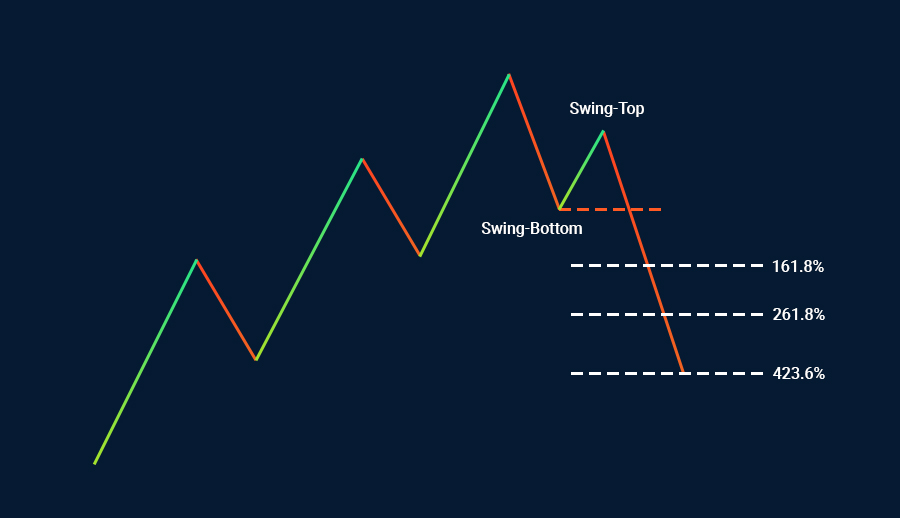
إيقاف الخسارة
في معرض حديثنا عن فيبوناتشي، فلنتناول مستويات جني الربح، على المرء ألا ينسى أن الأسواق لا تتحرك دائمًا في الاتجاه المتوقع. بل تتحرك أحيانًا في الاتجاه العكسي، لذلك ينبغي على المتداولين التخفيف من مخاطر خسارة المال من خلال إنشاء أوامر إيقاف الخسارة الواقية. بهذه الطريقة يمكن احتساب مخاطر خسارة المال مسبقًا. على سبيل المثال، ربما يتوقع المرء بعد الشراء أن يتجه السوق إلى الارتفاع، لكنَّ هذا لا يكون الحال دائمًا بالطبع. يدرك المتداولون المحترفون هذا الأمر جيدًا، ولهذا ينشئون أمرًا وقائيًا لإيقاف الخسارة، لعله تحدث أمور غير متوقعة.
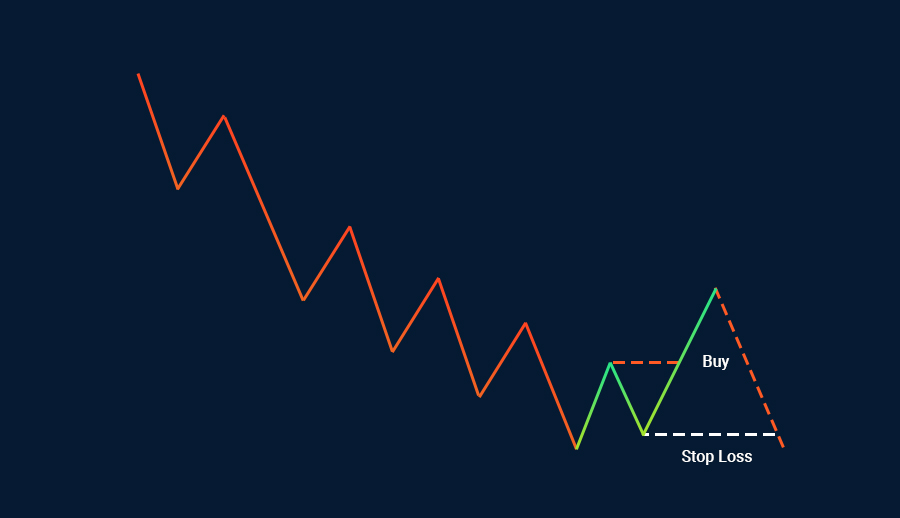
بالمثل، يجب أن ينتبه المتداولون بعد البيع إلى أنه لا يوجد شيئ مضمون في الأسواق بنسبة 100%؛ ومن ثم، يوصى باستخدام أمر إيقاف الخسارة للتخفيف من مخاطر خسارة المال.
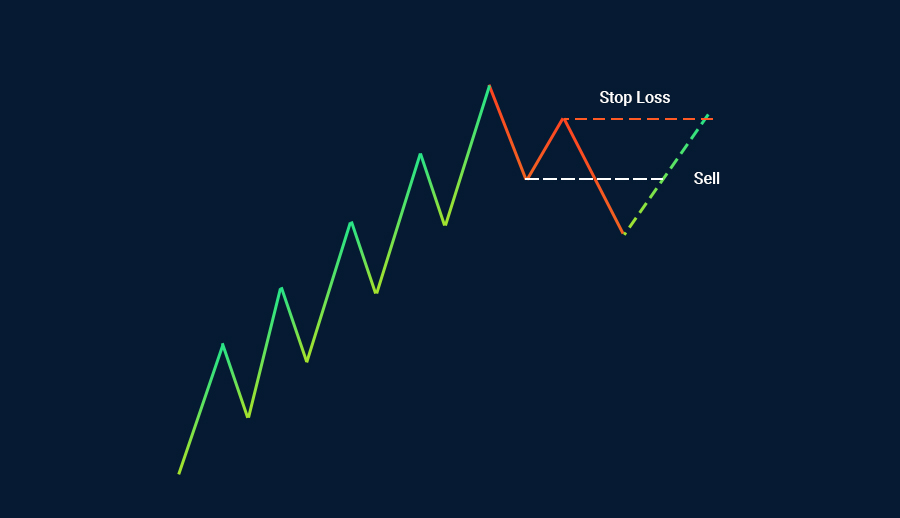
موجة إليوت
كذلك تُعَد امتدادات فيبوناتشي مبدءًا مهمًا تقوم عليه نظرية موجة إليوت. ربما تذكر أنه بحسب إليوت، فإن الأسواق تتحرك في خمس موجات.
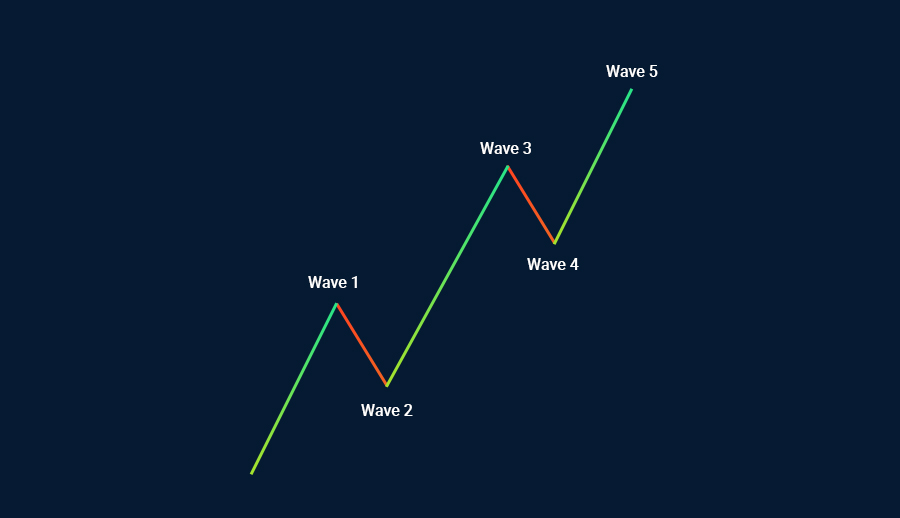
ربما تحدث الموجة الثالثة عند نسبة نحو 1.618 أو 2.618 أو 4.236 من الموجة الأولى. هذه بالفعل الموجة التي ينتظرها غالبية المتداولين. لماذا؟ السبب ببساطة يعتمد على النظرية القائلة بأنها ليست الموجة الأقصر على الإطلاق، لكنها عادةً ما تكون الموجة الأطول من الموجات 1 و3 و5.
الخاتمة
توجد أرقام فيبوناتشي والنسب المقابلة لها في كل مكان في الحياة، من الرياضيات إلى الطبيعة، ومن العمارة إلى الجسم البشري. حتى عندما يصف البعض وجود هذه النسب بالمصادفة، تظل من الممارسات المقبولة على الأقل لدى مجموعة من المتداولين أن يستخدموا امتدادات فيبوناتشي في تقدير السعر المحتمل ومستهدفات الربح أو الخسارة.
تعلم التداول مع FXTM
تعرف على كيفية اتخاذ قرارات التداول الصحيحة المناسبة لأسلوبك في التداول وأهدافك من خلال مجموعتنا الشاملة من المواد التعليمية. تعلم من المنزل في الوقت وبالكيفية التي تناسبك من خلال مقاطع الفيديو التعليمية أو اشترك في ندوة إلكترونية من على بُعد. كذلك نقيم ندوات ووورش عمل تفاعلية حول الفوركس في مختلف بلدان العالم. ربما تُعقَد واحدة في منطقة قريبًا.
إخلاء المسؤولية: تتكون هذه المادة المكتوبة/المرئية من آراء وأفكار شخصية. لا ينبغي تفسير المحتوى باعتباره يتضمن أي نوع من النصائح الاستثمارية و/أو الحض على القيام بأي معاملات. ولا ينطوي المحتوى على أي التزام بشراء خدمات استثمارية أو يضمن أو يتنبأ بما سيكون عليه الأداء في المستقبل. ولا تضمن شركة FXTM أو المنتسبين إليها أو وكلاءها أو مديريها أو مسئوليها أو موظفيها دقة أو صحة أو التوقيت المناسب أو كمال أي معلومات أو بيانات واردة ولا يتحملون أي مسؤولية فيما يتعلق بأي خسارة ناجمة عن أي استثمار تم على أساسها.
التحذير بشأن المخاطر: تداول المنتجات القائمة على الرافعة المالية مثل الفوركس والعقود مقابل الفروقات يحمل مستوى مرتفع من المخاطر. ولا ينبغي عليك المخاطرة بأكثر مما يمكنك أن تتحمل خسارته، ومن المحتمل أن تخسر أكثر من استثماراتك الأولية. ولا ينبغي أن تقوم بالتداول إلا إذا كنت تفهم فهما تاما المدى الحقيقي لتعرضك لمخاطر الخسارة. ويجب عليك عند التداول أن تأخذ في اعتبارك على الدوام مستوى خبرتك. إذا بدت المخاطر التي ينطوي عليها التداول غير واضحة بالنسبة لك، يرجى الاستعانة بمشورة مالية مستقلة.
